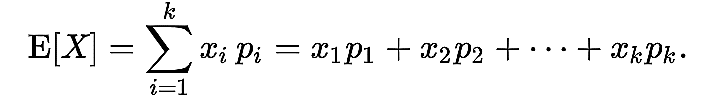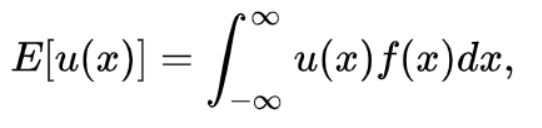Especially in crisis you will not have many decisions with a clarity about them. Thus, your ability to think in probabilities becomes incredibly valuable. By using probabilistic thinking your chances of success in a crisis will increase dramatically.

_____

In everyday life you will have to face multiple decisions - small and large - and most of the time you will have little trouble making them. In a crisis though you are taking important decisions daily and on top of that they will be urgent and complex. Complexity, urgency and importance make a very stressful combination and with higher stress your decision-making capacity will decrease. Each decision will deplete more of your willpower.

Now it becomes ever so important to have a structured way of going about your decisions. Not only the structure of your decisions is of great importance, also your whole way of thinking is. One of the most crucial skills is probabilistic thinking. Especially in crisis you will not have many decisions with a clarity about them, you will be lacking crucial information and you will not have the time to gather it. Thus, your ability to think in probabilities becomes incredibly valuable. By using probabilistic thinking and using a few other tools your chances of success in a crisis will increase dramatically.

The following content will use equations and concepts from behavioural economics and statistics and for it to be better digestible we shall introduce an example:

Imagine standing in front of a decision for your business. You are in a crisis and fighting for survival. You have two choices, one where you will get 1 million euro with a 100% certainty and one where you can gain 1 billion euro with a 50% chance of success. With the first option you can buy some time for your business to find a solution to solve your predicament. With option two you can solve your crisis, but only at 50% chance. Now before you read on, I want you to take some time to think about this and chose an option. This is for your own learning, so please do not cheat here.

100% chance to win 1 million, 50% chance to win 1 billion

Now that you have chosen an option, we can run through this example using some rules of behavioural economics and a little bit of creative thinking. One note beforehand, at all times when solving problems keep the Design Thinking process in mind. If you have not heard of this before, especially in times of crisis I recommend (oh what wonder) to read my previous article on this topic, which you can find here.

Before I begin to explain the different methods: A rule of thumb to keep in mind is that you will need to work with educated guesses. Often you do not have all the puzzle pieces and to create a full picture you will have to guess some of the pieces. To minimize your guessing being wrong it is important for the guesses to be “educated”. This basically means using any information you can find to extrapolate your missing piece. For example: If you do not have enough knowledge on your competitor to know how he will react, try to look at case studies and see how similar companies reacted to similar situations and formulate a probability from that.

Expectation Value (BAYES’ THEOREM)

For our case we will keep it very simple: The Bayes’ Theorem essentially calculates the value one can expect of a proposition or hypothesis based on available data and information.

Coming back to our example. If you would decide against the 1 million, the mathematical equation of the Bayes’ Theorem would look the following:

E = -1 M × 100% + 1 B × 50% = 499 M

Here we see that the potential gain of winning one billion far outweighs the potential loss of one million and thus we should choose the one billion option.

In psychological terms: When you try to gauge other players, you should try and find out what their expectations are. Say you are in a negotiation and the opposite party is expecting something and your offer underdelivers badly, your chances of success are not so good. But if you are close to their expectation you are more likely to succeed. Sometimes a good result may be interpreted as bad, only because the expectations were higher or vice versa. Just thinking about this can give you an edge in making decisions.

For those of you who are interested in understanding the behavioural mathematics behind this, here is the equation. You can find lots of detailed articles on this if you google the name of the theorem.

Expected Utility Hypothesis

Essentially the expected utility hypothesis (utility = satisfaction) tries to mathematically describe that people have different preferences. Here the important part is u(x), which states the value that is given to a certain outcome (x). Please note that we are talking about subjective preferences. In our example at the beginning you need to keep people’s preferences in mind - especially your own. If you are very risk averse you will probably prefer to take the one million because there is no risk (even if it might be the wrong decision in your case). Especially when you are trying to guess a competitor’s decision this theory comes in handy. If you for example know that he loves to take a good gamble, you can make the guess that his expected utility will be higher for high reward, high risk paths.

The Prospect Theory (KAHNEMAN)

2002 Daniel Kahneman received a Nobel Prize for his prospect theory, which is depicted in the graph above. As you can see, the positive value for a gain of 100 is far lower than the negative value of a loss of the same magnitude. Roughly speaking a loss hurts twice as much as a gain makes you feel good. In numbers this means, gaining €200 will be of the same emotional magnitude as losing €100. So, to balance the loss of € 100 you have to gain €200 back. This explains why people will sell an asset at 5% loss in panic and when their asset has gained 10% they hold onto it. Most people will need the potential winning to be far higher than the potential loss, if they have to choose between gaining versus potentially losing. In our example if say the second option were only 3 million (50% chance), most would not take the gamble. The one million loss hurts too much. The phenomenon explains also why we tend to be hard with ourselves. You expect yourself to win twice as often as you lose or win twice as much as you lose in order for it to feel “equal” or ”neutral”. Our perception concerning this is warped.

Using Game Theory

Another important step right at the start of the decision-making process is to ask yourself a few questions about the other players. In most decisions you will have several players (competitors, stakeholders, employees etc.) to keep in mind and you will need to understand their agendas, which will require for you to do your research and to have a good amount of empathy.

Are the actors in the situation rational?
Are we able to reach a Nash Equilibrium?
Do they act according to self-interest?
Do they understand the rules of the game?
What is their dominant strategy?
And is their dominant strategy really dominant?

Let us have a look at our example and introduce a second player. So far, we only had to think about our own preferences and our own situation. But it gets far more interesting if we for example are reliant on a competitor’s choice.

In the game theory table below, we have listed the choices of each player and the outcomes. Imagine that your competitor and you are both facing the same choice, with the difference that dependent on the others choice there are slightly different outcomes. If you choose the one million option and your competitor chooses the same, you both get nothing. If you both choose the one billion option, you both get half a billion (at 50% chance). If you choose the opposite of the other, you get either one million or have the chance of 50% of getting the full billion.

Now what do you do? In this case the Nash equilibrium would be, that both players take the one billion. If you play it safe, you run the risk of not getting anything. It would therefore not make sense to opt for the safe option, unless you have 100% certainty that the other player will opt for one billion.

This basically shows how making a decision can become more complex once other players are involved. Another point to note is that often the best solution for oneself is by striving for a win/win solution with your opponent.

Creative Alternatives

Now that we have run through the thought processes using behavioural economics and probabilities, we can have a look at some outside the box solutions to the portrayed problem. Leading a company is not a question of black and white thinking. As explained earlier on, you often do not have the full picture and due to many players in the game, there are no right and wrong decisions. Keep a creative mindset and you will always find a good or excellent solution. Below I have listed a few possible options for how to go about the example in the introduction.

Sell the option of winning 1 billion for a fixed sum or a dividend. You can increase your cashflow by selling the option for a dividend and this could safe you on the long run, or you sell the option for say 20 million, if 20 million is enough to safe the company.

Sell the option of winning 1 billion for a fixed sum and use the money to take on leverage (get a loan from a bank or investor) to finance the turn around.
Use the option of winning 1 billion to leverage other parties into contracts with you, which will make your survival certain. With the possibility ahead some customers or other stakeholders might be compelled to do business with you. This can give them the confidence that was prior missing.
Use the option of winning 1 billion to increase the sale value of your business. An option like this can be used as great leverage when selling your business. Some buyers will pay extra and take the gamble.
Get a private equity partner, who is willing to invest in your business for the chance of big gains. Private equity investors are inclined to invest on bets, and a 50% bet on making 1 billion is quite good odds in private equity terms
Do a lottery. You could sell the option in lottery tickets and use the proceedings of the lottery to finance the turn around.
You could use Brinkmanship and leverage the option with your creditors: “Either you give me a haircut and I will survive due to this amazing option or I go bankrupt.“ This is a last resort option, but use this with caution. Do not do this if you are not ready to go through with it. Brinkmanship is like making a threat. Never make threats that are empty. Your creditors might agree to a 30% haircut, if there is a high chance that they get at least 70% back. And a 50% chance is quite good for a company in crisis.

Tools and Tips

There are some other tools that can help you with thinking in probabilities, I will quickly share these with you now. I used all of these in managing our crisis back in 2015. There were quite some complex relationships and processes to keep in mind. Moreover, we had many different parties to take in account, when making any decisions.

The first tool that I found extremely helpful was to draw up a Relationship Diagram of all the people involved. This gives you a great overview of who is involved with whom in what way. Due to the large number of players in our case, we kept it quite simple and assigned each player one of three relationship types (cooperation, enmity and neutral). The less players you have to take into account, the more different relationship types you can introduce. Although sticking with Pareto, I personally think that 3 relationship types is enough to give you a really good overview.

I can warmly recommend using Decision Trees. Many decisions that people make are sequential and using a decision tree you can depict the decision processes really well. It will show you the consequences of certain decisions and the path that it will entail. If decisions happen in parallel a game theory table is the better option. Below I have added a simple example of a decision tree. It is a pretty mundane example, but it will do for you to get the idea. It’s the process of deciding if you should eat and where to eat. Obviously in a crisis scenario or any important decision scenario the tree will be more complicated since the decisions that are to be made are more important than knowing if you should buy a hamburger or not. You can use decision trees not only for depicting your decisions, but also for other people’s decision-making processes.

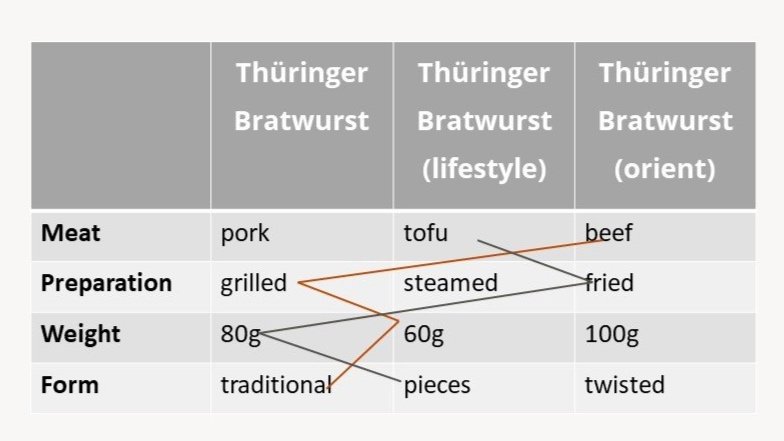
Morphological Boxes is a great tool, that is widely used in engineering. They go incredibly well together with scenario planning. I love to plan scenarios - maybe a bit to obsessively. I personally think if you can imagine 50 out of 100 possible scenarios, you have already reduced the probability of being surprised down to 50%. Not bad, right? So again, I have added a mundane example of a morphological box below. This time we will discuss a traditional German sausage - the Thüringer Bratwurst. But before we get into making sausages, let’s talk about morphological boxes in general. Usually in engineering you have several functions/parameters that a product has to account for. For each function/ parameter you tend to have several ways of solving for it, this will make for many different solutions. Some of the solutions are compatible with each other and some are not. In order to depict this in a good way, you use a box as below. You can draw up possible solutions using different colours. This does not only apply to products such as sausages but also to scenarios.

Above I already mentioned Scenario planning as something that I personally love to do. Scenario Planning is a method wildly used in strategic planning in the military or in disaster management. But it is also incredibly valuable for any business scenario, especially in a crisis. In this article we talked about thinking in probabilities and some methods of probabilistic thinking that can help with this. But probabilities themselves are only a glass half full. In order to understand your options, you need to have a good overview of the possible scenarios. Once you have them sorted you can put probabilities to each of them. In the example we went through we have two scenarios, and each has several different sub scenarios (especially when we get creative). Scenario planning can fill up a whole article and there are many good articles online, just google scenario planning. Below nevertheless I have listed a check list for how to approach it. Give it a go when you are stuck with a decision or you are having a hard time sorting through your options.

Decide on the key question to be answered by the analysis.
Set the time and scope of the analysis.
Identify major stakeholders.
Map basic trends and driving forces.
Find key uncertainties.
Check for the possibility to group the linked forces.
Identify the extremes.
Define the scenarios.
Write out the scenarios.
Assess the scenarios.
Identify research needs.
Develop quantitative methods.
Converge towards decision scenarios.

Once you start to consider probabilities and what consequences certain decisions can have, the picture for the right path becomes much clearer and it is less of a gut feeling decision. Experienced leaders get good at assessing probabilities and can decide on a gut feeling, as their subconscious processes the data they have at hand at an incredible speed. Be careful thou. Your subconscious is mainly based on past experiences and things you learnt. This can be extremely dangerous in times of change. I highly suggest using structured thinking if you can.

How to Incorporate Probabilistic Thinking into Decision-Making